DISCRETE FOURIER TRANSFORMATION(DFT)

In this post we are gonna learn about fourier transformation and implementation of Discrete fourier transformation in python.

Why we need to use fourier transformation anyway...a normal periodic wave like sine wave has 3 characterstics like Phase,amplitude,frequency that tell us about the wave..it's easy and understandable but what if a wave is unperiodic like this ex.

in this example it is not a periodic sinewave..so but an multiple frequencies of waves added together. Hence to analyse these kind of waves we need fourier transformation in signal processing. The fourier transforamation is applied in both Continous and Discrete waves..In this we are gonna concentrate in DFT(Discrete fourier transformation)..and to visulalize the wave we are gonna use python(cause it's easy to use).

we need the following python library to do this :

1.numpy    2.seaborn    3.mathplotlib    

DFT(DISCRETE FOURIER TRANSFORMATION)

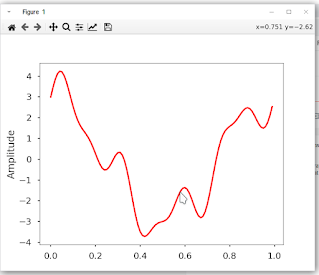
It is applied to specifically discete signals. It is used to break the unperiodic wave into bunch of sinusoids and cosine waves for analysis. Using DFT we can split a wave like above picture into bunch of sinusoids spectrum like this.

The DFT is used to convert Time Domain into frequency Domain and vice versa.

DFT is defined as 

where                                                                                 

N = no.of samples 

n = current sample

K = current sampling frequencyxn = the sine value at sample 

xn = The sine value at sample n

Xk = The DFT in which the real and imaginary values a wave with Amplitude and phase info

In here the nature of equation is  Xo = Σxn , tells us If N in ODD then, X1,X2...X(N-1)/2 contains the positive frequency and  X(N+1)/2.....XN-1 in negative frequency in decreaing order. If N in EVEN then, X1,X2,...,XN/2-1 contains positive frequency and the elements XN/2.. .XN-1 in negative decreasing order.

The Xk gives the both real and imaginary numbers so to get amplitude and phase we need this formula.

Here the atan2 means the arcTan of 2 like 

Here is the code for DFT python function creating a 1Hz and 4Hz , 7Hz waves addition and DFT :

import numpy as np

plt.style.use('seaborn-poster')
#matplotlib inline

# sampling rate
sr = 100
# sampling interval
ts = 1.0/sr
t = np.arange(0,1,ts)

freq = 1
x = 3*np.cos(2*np.pi*freq*t)

freq = 4
x += np.sin(2*np.pi*freq*t)

freq = 7 
x += 0.5* np.sin(2*np.pi*freq*t)

plt.figure(figsize = (8, 6))
plt.plot(t, x, 'r')
plt.ylabel('Amplitude')

plt.show()


def DFT(x):
    """
    Function to calculate the 
    discrete Fourier Transform 
    of a 1D real-valued signal x
    """

    N = len(x)
    n = np.arange(N)
    k = n.reshape((N, 1))
    e = np.exp(-2j * np.pi * k * n / N)
    
    X = np.dot(e, x)
    
    return X

X = DFT(x)

# calculate the frequency
N = len(X)
n = np.arange(N)
T = N/sr
freq = n/T 

plt.figure(figsize = (8, 6))
plt.stem(freq, abs(X), 'b', \
         markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.ylabel('DFT Amplitude |X(freq)|')
plt.show()

n_oneside = N//2
# get the one side frequency
f_oneside = freq[:n_oneside]

# normalize the amplitude
X_oneside =X[:n_oneside]/n_oneside

plt.figure(figsize = (12, 6))
plt.subplot(121)
plt.stem(f_oneside, abs(X_oneside), 'b', \
         markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.ylabel('DFT Amplitude |X(freq)|')

plt.subplot(122)
plt.stem(f_oneside, abs(X_oneside), 'b', \
         markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.xlim(0, 10)
plt.tight_layout()
plt.show()

Here are some additional info on DFT and blogs