The Loss function/Cost Function

In this post we are gonna learn about the loss function in machine learning..The loss functions are essential in machine learning cause they are one who tells the algorithm if it makes mistake in prediction as wrong.

so The Loss function/Cost Function are integral part of gradient descent and entropy calculations. Here we are gonna learn a bit about the different cost functions for different types of problems in machine learning.

Mathematical Formula for Entropy :

Consider a data set having a total number of N classes, then the entropy (E) can be determined with the formula below:

Where:

P_i = Probability of randomly selecting an example in class I;

Entropy always lies between 0 and 1, however depending on the number of classes in the dataset, it can be greater than 1. But the high value of Let's understand it with an example where we have a dataset having three colors of fruits as red, green, and yellow. Suppose we have 2 red, 2 green, and 4 yellow observations throughout the dataset. Then as per the above equation:

===>   E    =    −(Prlog2Pr+Pglog2Pg+Pylog2Py)

Where;

• P_r = Probability of choosing red fruits;          P_g = Probability of choosing green fruits and;
• P_y = Probability of choosing yellow fruits;    P_r = 2/8 =1/4 [As only 2 out of 8 datasets represents red fruits];
• P_g = 2/8 =1/4 [As only 2 out of 8 datasets   represents green fruits];
• P_y = 4/8 = 1/2 [As only 4 out of 8 datasets  represents yellow fruits];

  

Now our final equation will be such as;

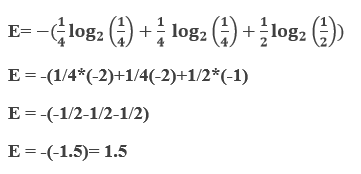
So, entropy will be 1.5.

Let's consider a case when all observations belong to the same class; then entropy will always be 0.

E=   - (1log2 1)   = 0

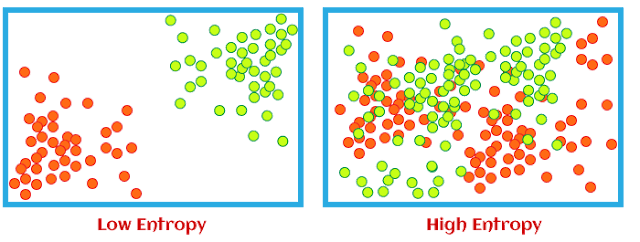
When entropy becomes 0, then the dataset has no impurity. Datasets with 0 impurities are not useful for learning. Further, if the entropy is 1, then this kind of dataset is good for learning.

Cross-entropy loss, or log loss, measures the performance of a classification model whose output is a probability value between 0 and 1. Cross-entropy loss increases as the predicted probability diverges from the actual label. So predicting a probability of .012 when the actual observation label is 1 would be bad and result in a high loss value. A perfect model would have a log loss of 0.

LOG LOSS FUNCTION(CROSS-ENTROPY) :

The graph above shows the range of possible loss values given a true observation (isDog = 1). As the predicted probability approaches 1, log loss slowly decreases. As the predicted probability decreases, however, the log loss increases rapidly. Log loss penalizes both types of errors, but especially those predictions that are confident and wrong!

Cross-entropy and log loss are slightly different depending on context, but in machine learning when calculating error rates between 0 and 1 they resolve to the same thing. In binary classification, where the number of classes M$M$ equals 2, cross-entropy can be calculated as:

Normally the log loss function in simplified form is : 

H(q) =  −(ylog(p)+(1−y)log(1−p))

But for the binary classification the formula can be modified a little bit hence :

For More Information please check this awesome post.